数学老师曾告诉我们,只有收敛的级数才能求解无穷项之和,然而在一些科普书中,却会遇到一个神奇的求和:
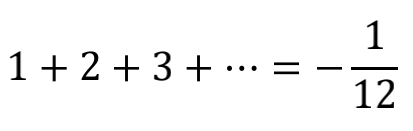
所有自然数之和怎么会是负数,而且还是个分数?这到底是人性的扭曲,还是道德的沦丧?
把对称轴当作级数和
想要理解这个古怪的结论,我们先来看一个简单的例子:1, -1, 1, -1, ……这个序列可以求无穷项之和吗?意大利数学家格兰迪(Dom Guido Grandi,1671-1742)早在1703年就开始认真琢磨这个问题,可以说,这是所有发散级数求和研究的起点,这个序列后来就被命名为“格兰迪级数”。

意大利数学家格兰迪丨图源:维基百科
也许有小伙伴猜测,这个序列中1和-1的数量既然同样多,那么总和就应该等于0。可惜这样的猜测是错误的。无穷集就像个再生能力很强的变形虫,部分与整体同样多。我们从序列中拿走任意个1或者-1之后,剩下的1和-1数量仍然相同。如果所剩下的1和-1加和为零的话,那么岂不是总的求和仅由先取出的1或-1的数量决定——也就是任意整数。这显然太不靠谱了,看来压根不能依靠比较1和-1的数量来求和。
还有个办法,就是借助收敛的级数寻找线索。我们知道,在|q|lt;1时,
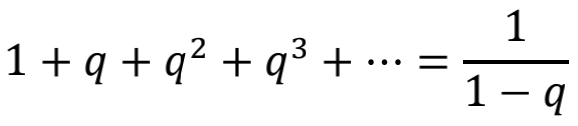
现在我们粗暴地让q=-1,于是就出现了
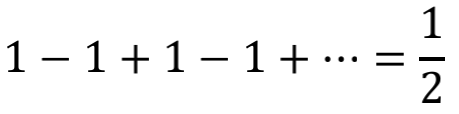
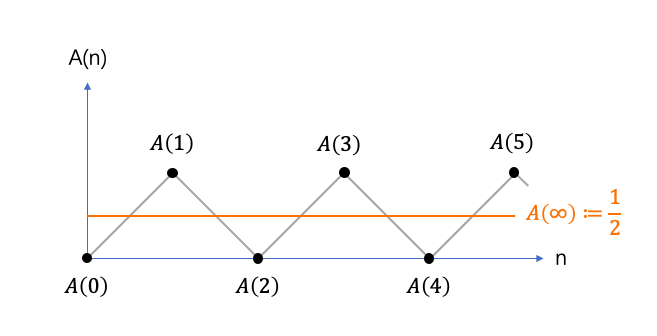
这个结果似乎还能令人接受,可是,q=-1毕竟是个“不合法”的条件,我们需要更合理的途径来安抚内心的不安。如果把这个级数的前n项和记做A(n),我们现在动手来求 A(∞)。
哈!根据这个等式,我们又一次得到了 A(∞)=½ 的结果。这回貌似没有明显违法的地方了,警察来了也不怕。可是,总还是感觉哪里不对。
A(1)=1
A(2)=1-1=0
A(3)=1-1+1=1
…
可以看出A(n)在1和0之间来回跳动,按照极限的定义,
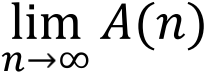
相关的定义不止一种。大体来说,主要有切萨罗求和与阿贝尔求和两类,另外拉马努金和黎曼等人也发展出许多更一般性的理论,中间还掺有源自欧拉的诸多贡献。那些数学语言虽严格,但催眠和劝退的副作用也不小,所以本文不打算纠结于那些从集合论谈起的基础定义,只使用非常“物理”的视角来定义: A(∞)表示所有 A(n)的平均值。
以“平均值”定义的求和方式,使许多发散级数都可以进行求和。例如
1-2+3-4…
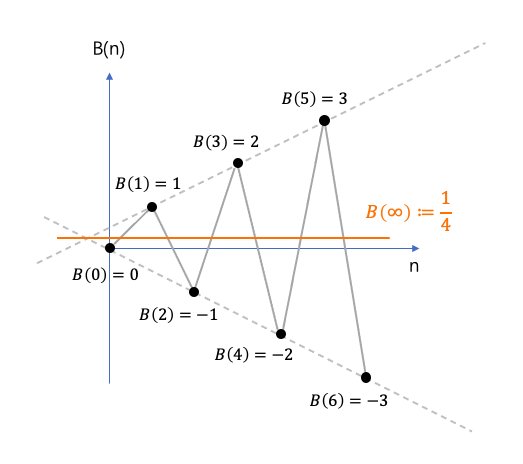
这个级数,也可以用同样的方法直接用眼睛瞪出结果。我们用B(n)表示前n项和,即 ,那么
B(0)=0
B(1)=1
B(2)=1-2=-1
B(3)=1-2+3=2
…
把这些B(n)所对应的点画在图上之后,完全不需要动笔计算,用眼睛就可以直接看出所有B(n)的平均值是1/4。
如果只看图还不放心,我们也可以借助前面 A(∞)=½ 的结论来推算 B(∞):
稍微调整等式右边的计算顺序,先让前面括号内第n项减去后面括号内第n项,然后再做加和。
即
A(∞)-B(∞)=B(∞)
所以
B(∞)=½A(∞)=¼
把自然数之和变成-1/12的魔术
当然,画出点来再用眼睛直接瞪出结果的方法,有时候也需要一些技巧。就以全体自然数之和为例,我们同样地令C(n)代表前n项和
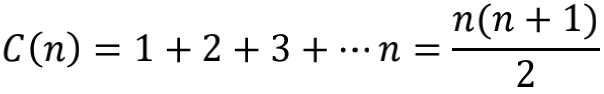
麻烦出现了!显然C(n)对应的点都分布在一根上扬的抛物线上,没办法直接看出平均值,而且看起来压根就不存在有限的平均值!别急,我们可以继续变形。
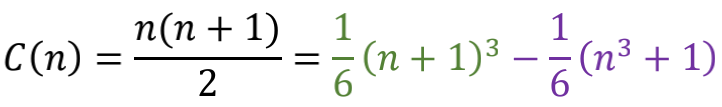
这样我们就把每个C(n)对应的点,都拆成上式中绿色项和紫色项所对应的两个“半点”分别画出来,居然又可以凑成两条对称的曲线。
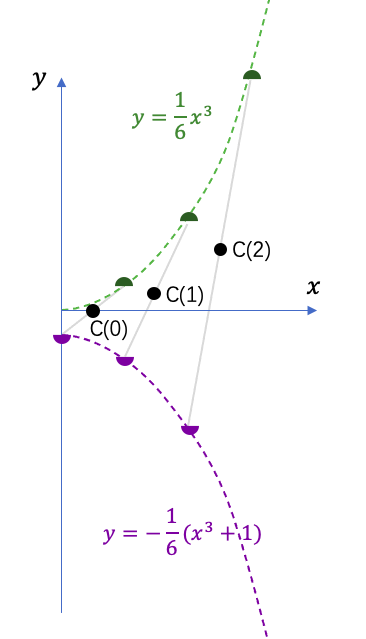
当我们把无限个“半点”都辛苦画完之后。就可以指着两根曲线中间的对称轴宣布:
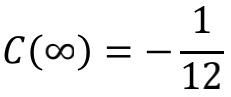
因为所有C(n)的平均值就等于所有“半点”的平均值,而两根曲线上的“半点”分布完全对称,只在绿色曲线的开头位置差了一个无关紧要的0。
除了看图猜值,我们也可以借助刚才的 B(∞)=¼ 那个结果,再来计算一遍 C(∞)。
调整顺序后
于是得到
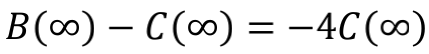
所以
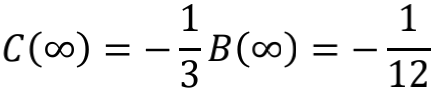
其实,能够得到 -1/12 这个结果的途径还有许多。例如神奇的Zeta函数
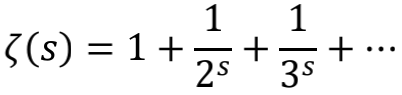
这个以复数s为变量的函数,因著名的黎曼猜想及其与数论的紧密联系而被反复研究。数学家们可以写出这个函数的许多种变化形式,其中一种解析延拓到全部复平面的形式是
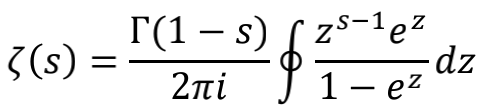
用这个形式也可以计算出
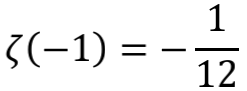
既然经过这么多五花八门的方式,都殊途同归到 -1/12 这个结果,我们是不是可以把 1+2+3+…=-1/12 这个式子堂而皇之地写进中学课本中呢?相信许多人会跟我一样,对此仍惶恐不安。因为在前述所有推演过程中,都埋藏着一个颇为隐蔽的问题,那就是等号的意义。将
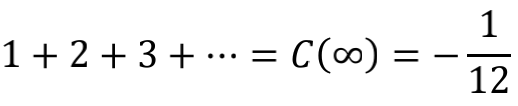
或
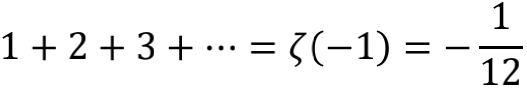
直接写成
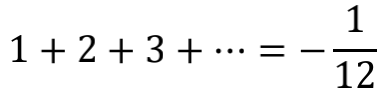
似乎理所当然,但其实两个式子中,前面的“=”代表的是“定义为”,而不是量值相等。所以,更清楚的写法应该是
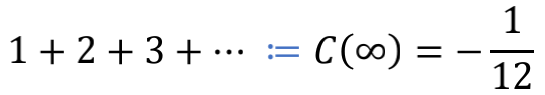
和
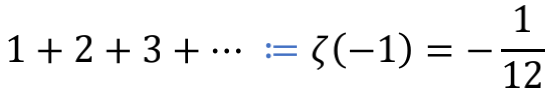
这样就能看出,-1/12 这个数值,并不像1+1=2那样自然天成理所应当,而是需要事先假定“全体自然数之和是一个确定的数”,然后再精心挑选出一个逻辑自洽性最好的数值,指定其为全体自然数之和。只不过当逻辑自洽性和直觉发生明显冲突的时候,我们都会感觉惊诧,这在数学发展的道路上已经不是什么新鲜事了。
伸向无穷大的剪刀
前面的讨论中,我们直接无视了数学极限概念,粗暴地使用平均值当做发散级数的和。现在让我们重新捡起极限概念,从另一个角度看看-1/12是怎么跑出来的。
对 C(n) 这个发散级数,我们可以引入某个剪刀函数 f(x) 来压制那些趋向无穷大的项,从而使发散的趋势在某个特定的位置N附近停下来,并最终收敛到某个极限S(N)。这样我们就用标准的极限概念构造出一个S(N),当N有限时,S(N)是个有限值,而当N趋于无穷大时,S(N)就对应着全体自然数之和。
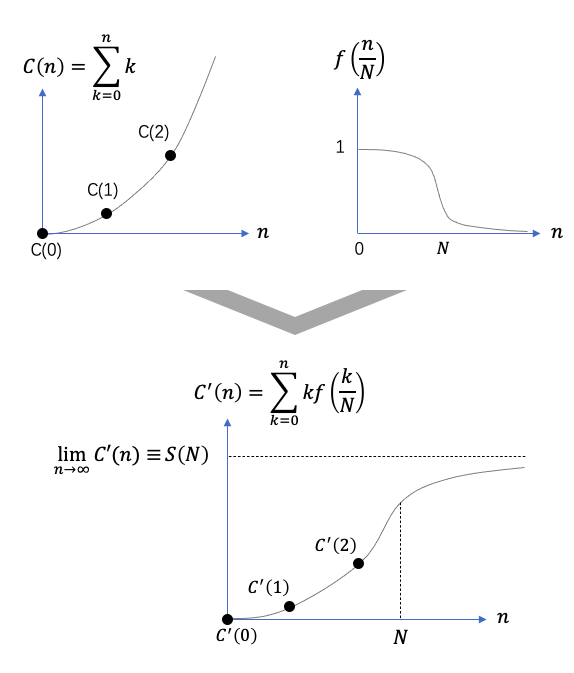
可以充当剪刀的函数有许多,比如我们取
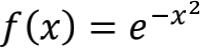
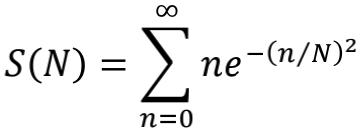
通过数值计算,我们发现S(N)随着N的增加而奔向正无穷。这倒是符合我们先前的直觉了,可是说好的-1/12呢?别急,我们再把S(N)用1/N展开看看。我们发现S(N)在大N的数值结果,可以被下面的展开式很好的拟合
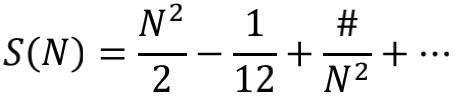
哈!居然又看到了这个-1/12,它是S(N)展开式中的常数项。也就是说,在S(N)中与N的变化无关的成分,就是-1/12。当N足够大时,那些含1/N的项都可以忽略,S(N)可以被看做一根最低点在-1/12处的抛物线。
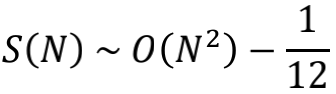
我们再取剪刀函数 f(x)=e-x 试试。此时
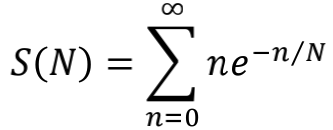
这个求和可以严格计算出来。我们先对下面的等式两边求β的导数
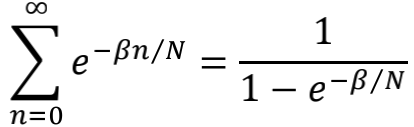
可以得到
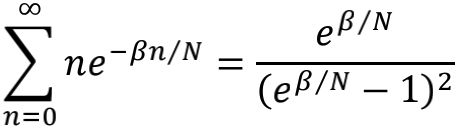
同样在大N条件下做1/N展开,就得到
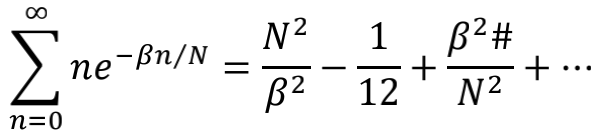
取β=1就得到
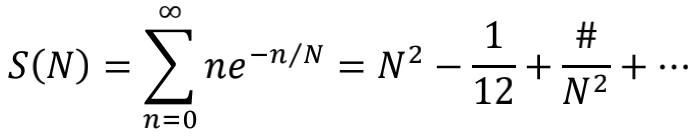
同样也出现了常数项-1/12,而且也是根下垂到-1/12处的抛物线
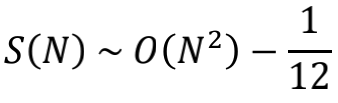
如果 f(x) 直接取为跳变函数,也就是在 n=N 处突然截断,那么
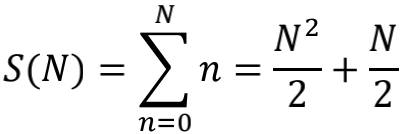
就不会有-1/12这个常数项。
看起来,除了跳变函数的突然截断,其他平滑的截断方式都能得到
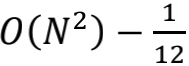
真空的能量
站在实用的视角来说,我们有时候需要像使用收敛级数一样处理自然数之和,所以就不得不找到某个确定的“缰绳”来驾驭。比如在研究真空能量的时候,物理学家就遇到了全体自然数之和,而且非常希望这个和是个确定的数。
在量子场论的理论模型中,真空就像一张立体弹簧网,由无数小弹簧横纵交织而成。而所谓粒子,就是其中某些小弹簧的振动足够剧烈,以至于远远望去以为弹簧网中出现了什么异物似的,但只要凑到近处就会看出,那里除了振动本身别无他物。也就是说,粒子本质上就是真空的振动。因此,当能量变化时,粒子的数量不必受任何守恒律的约束,可以凭空增加或者减少。不过,粒子能否产生或消失却与小弹簧的振动频率有关。在振动频率为ω时,粒子数n与场的能量E之间存在这样的关系:
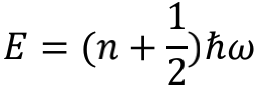
从关系式可以看出,真空每攒够一份ћω大小的能量,就会产生出一个粒子;反之每减少一份就会擦除一个粒子。或者干脆说,每个粒子其实就是个ћω大小的能量包。有趣的是n=0时,它对应着真空里没有粒子的情况,此时能量是½ћω。也就是说,当真空的能量低到不能再低的时候,能量仍然不是0,这就是真空零点能。下面我们来具体计算一个有限空间内的真空能量,看看它与全体自然数求和到底是什么关系。
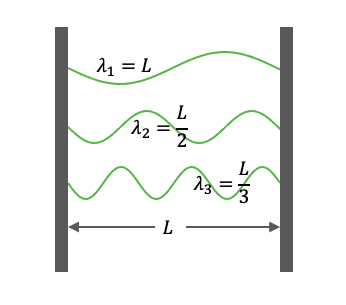
我们知道,两端固定的弹簧上只能存在驻波,即波长的整数倍恰好等于两端距离的波,因为只有这种波在来回反射过程中可以维持能量,其他形式的波都会自我消减。导体对于电磁场也有一模一样的作用。在距离为L的两块金属板之间,只能存在波长恰好为 λn=L/n 的电磁波,其中n是正整数。每个这样的电磁波频率为
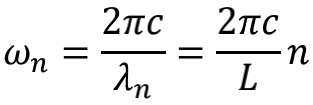
将所有频率的零点能累加起来,真空中总能量就是
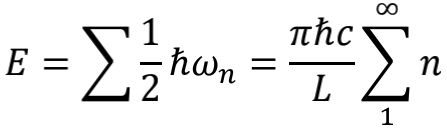
瞧,自然数之和 就这样出现了,现在你应该能够理解,物理学家们是多么希望 是个确定数值了吧。更有意思的是,如果姑且憨憨地认为自然数之和就是-1/12的话,我们甚至可以设计一个物理实验来验证这个结论。
如下图这样放置三块相互平行的金属板,使甲乙之间距离为a,乙丙之间距离为b。
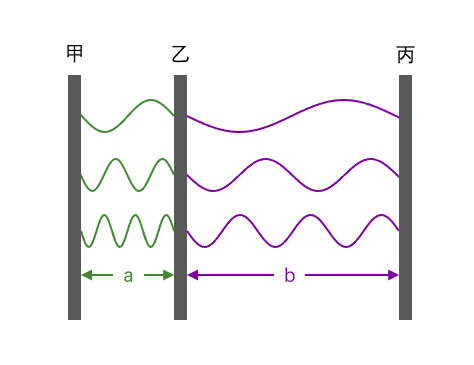
根据刚才的结论,我们知道甲乙之间的真空能量是
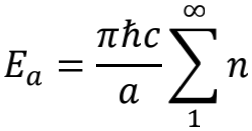
乙丙之间的真空能量是
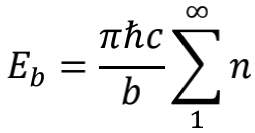
现在我们想知道,当a<b时,中间位置的金属板乙会受到哪个方向的力。根据能量对位置的偏导可以求解受力情况。结果发现:如果
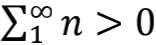
其实,实验装置还可以进一步简化,我们可以把最右边的丙拿到无穷远处,只留下甲和乙,然后测量甲乙之间是吸引还是排斥,如果相互排斥,就说明
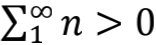
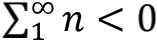
这个实验设想最早由荷兰物理学家卡西米尔(Hendrik Casimir,1909-2000)在1948年提出,当然提出实验的目的才不是测量自然数之和,而是为了验证真空零点能的存在。事实上,卡西米尔当年在提出这个实验的时候,就已经预言两金属板之间相互吸引,也就是对应
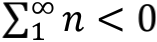

需要澄清的是,卡西米尔效应的实验证实,只能说明真空零点能的存在,但是并不能真的用来验证数学意义上的所有自然数之和。其实,现实中的金属板只能阻拦有限频率范围内的电磁波,当频率大过某个数值时,金属板就无法阻拦这种极高频率的波。所以从更精确的角度计算卡西米尔效应时,需要考虑这种高频截断。不过具体计算会用到欧拉-麦克劳林公式和伯努利数这些催眠的内容,本文就不再涉及了。
下面我们转到弦理论,看看所有自然数之和是如何与维度的数量产生关系的。
时空的纬度
前面提到,两端固定的一根弹簧之上只能存在驻波,所有振动频率只能是最低频率的整数倍。对一根两端完全自由的弦来说,结论同样成立。两端固定意味着端点速度为零,而两端自由则意味着端点的加速度为零。二者之间的差别,无非就是傅里叶分解时该写成
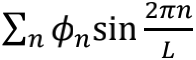
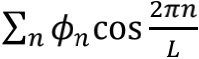
另外,弦理论中的量子化方式与量子场论所使用的技术手段如出一辙,所以同样存在
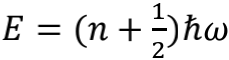
注意,仅具有最低能量的弦不会被当做粒子看待,只能被视为真空。表现为一个光子的弦,至少需要高出基态能量一份大小ћω1的能量。这份能量在一个空间维度上以光速传播,就是一个光子。根据相对论,在这个光子传播的维度上,不再具有振动的自由度,而剩下的空间维度里,弦都还具有基态能量。
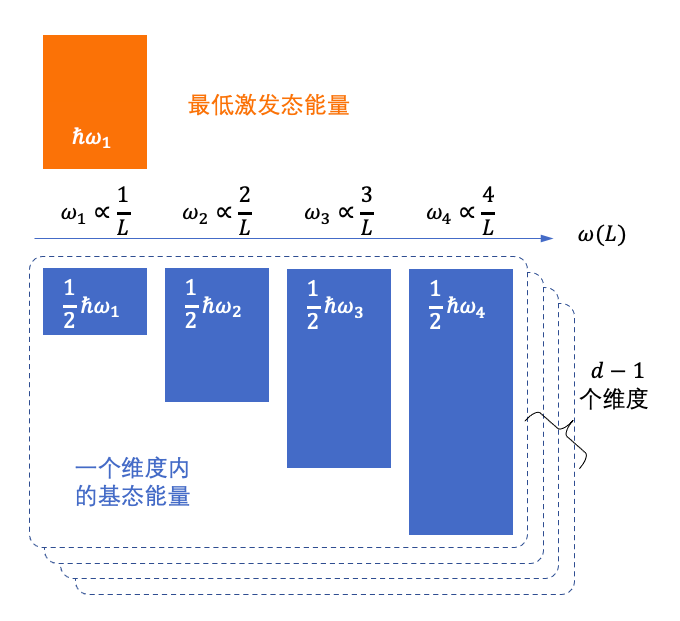
假设空间维度数是d,那么一个被激发成光子的弦所具有的最低总能量就是
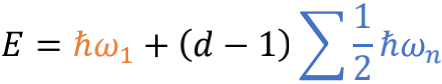
注意到 ωn=nω1 ,这个光子的总能量就变成了
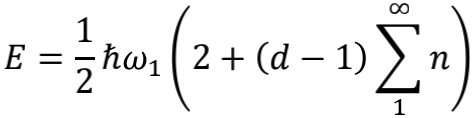
妥妥的又出现了 。
相对论告诉我们,光子的最低能量应该是零,所以跟相对论兼容的弦理论必须满足
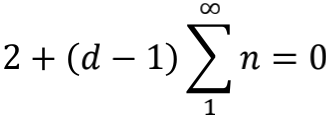
推演到这里,我们就要祭出
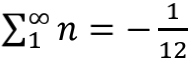
在超弦理论中,由于超对称因素的引入,弦的基态能量提升为3倍,光子能量约束条件变成了
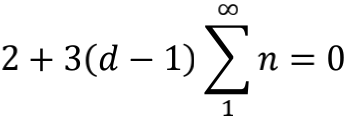
由此求出d=9,加上一个时间维度,总共凑成10维的时空。
以上就是玻色弦理论要求25+1维时空,以及超弦理论要求9+1维时空的故事梗概,希望读者能借助这些实例,对自然数之和在物理中的作用建立一些具像理解。
离散的时空
为了保持话题的收敛性,前文论述中刻意略过了许多有趣的细节。例如在弦的基态振动模式中,如果存在
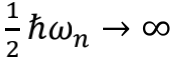
之所以能产生无限大的频率,就是因为我们允许存在无限小的波长。那么自然就会意识到,可以消除“紫外灾难”的理论模型中,空间必然存在有限的最小尺度。更直白地说,就是空间不可能是连续的舞台,而必须是离散的梅花桩。这个最小尺度究竟是多少呢?一个天然的候选者,当然就是普朗克长度。
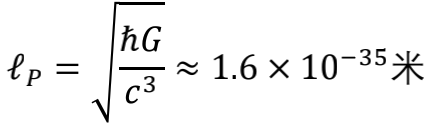
如果某个粒子的波长比普朗克长度还要短,那么这个粒子就会由于具备了太高的能量而把自己就地变成黑洞,而且这个黑洞所覆盖的区域又会超出普朗克长度。于是,普朗克长度就成了现有理论中最为自然的时空基本像素。
现在让我们抱持着离散时空的观念,重新审视卡西米尔效应实验。首先,任何距离都必须是的整数倍。那么甲乙板间距离a和乙丙板间距离b,就变成了
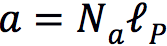
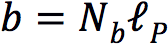
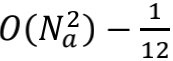
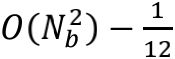
于是,先前的
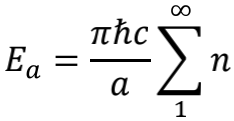
就变成了
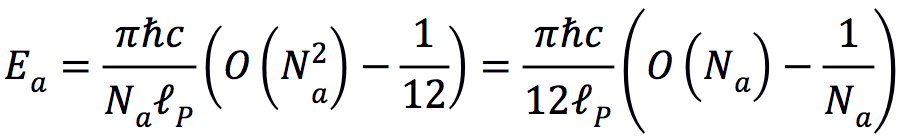
我们发现,甲乙板间的能量 Ea 分为两部分,其中一部分与 Na 呈正比,另一部分则呈反比。乙丙板间的能量 Eb 也是同样情况。
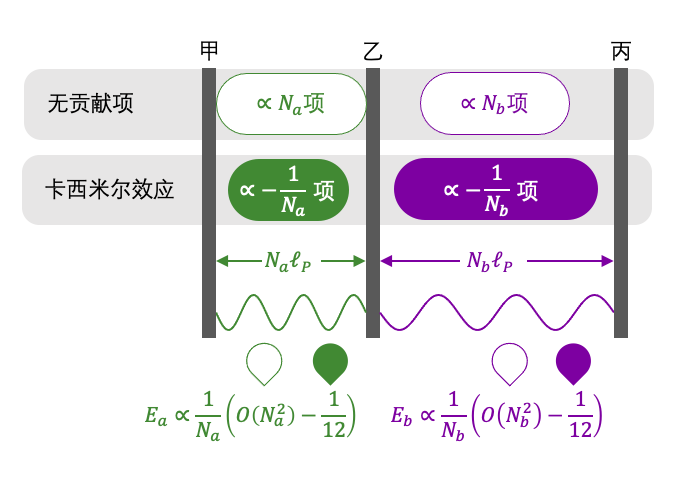
显然,呈正比的那部分能量,在乙板左右产生的作用力始终相互抵消,只有第二部分呈反比的能量,才对乙板产生了作用力。由此可见,卡西米尔效应是在两个巨大的首项恰好相互抵消之后,在第二项上显现出的效应,所以这种力异常微弱,只有把两个面积达平方米量级的金属板靠近到微米距离时,才能产生可供测量的吸引力。
现在我们才算真正解释了卡西米尔效应与自然数之和的关系,如果未来再遇到有民科企图用这个实验来证明自然数之和是个负数,尽可以毫不犹豫地送他一个白眼。
原文标题:所有自然数之和是-1/12?它在物理学中还有特别的应用?
来源:返朴
编辑:yrLewis
| 留言与评论(共有 0 条评论) “” |