一、莱布尼茨的一生
莱布尼茨是一位兴趣广泛、博学多才的大家,除哲学和数学外,他在历史、法学、语言、神学、逻辑学和外交等方面都有杰出的成就。下面我们简要回顾莱布尼茨的一生。

图1 莱布尼茨
1
才华横溢
1661年,莱布尼茨15岁,在莱比锡大学学习法律。直接读大二,三年获得学士学位,次年1月获得硕士学位。1666年20岁时,莱布尼茨已经为取得法律博士学位作好了充分准备。莱比锡大学的教师们由于嫉妒而恼怒,拒绝授予莱布尼茨博士学位,公开的理由是他太年轻,实际原因是他知道的法律知识比他们这些迟钝的家伙所知的加在一起还要多。他一气之下离开莱比锡赴纽仑堡附近的阿尔特多夫(Altdorf)大学。1666年11月,他凭借一篇讲授法律的新方法(历史方法)的论文(实际上是在从莱比锡赴纽仑堡旅途中写出来的)获得了阿尔特多夫大学的法学博士学位。但他谢绝了这所大学对他的聘请,参加了当地的一个团体(据称是炼金术士团体),并通过该团体结识了一些政界人物,从此莱布尼茨开始投身政治。他的第一份任命就是被选帝侯指定去订正法典。[1]
2
热衷政治
莱布尼茨一生余下的40年是在为不伦瑞克家族毫无价值的服务中度过的。他作为这个家族的图书管理人、历史学家和家族的总智囊,总共为三任主人服务过。对于这样一个家族,有一部光辉详实的家族史乃是极其重要的事情。莱布尼茨作为家族图书管理人,不仅是作为书籍的编目人,同时也是家系学专家和发霉的档案的搜集者。他的职责是确证他的雇主对欧洲半数王位的权利要求,如果不能确证,就通过审慎的篡改来炮制证据。为了进行细致的历史研究,他在1687-1690年跑遍了整个德意志,然后又去了奥地利和意大利。[1]
3
马车学术
莱布尼茨一生的特点之一:他具有在任何时候、任何地点、任何条件下工作的能力。他不停地读着、写着、思考着。他的大部分数学著作,更不用说其他关于一切事物的来世今生的作品,都是在既颠簸又四处透风的破马车里写出来的。当他在雇主反复无常的吩咐下东奔西跑时,就是这样的破马车载着他在17世纪欧洲的崎岖小路上奔波。[1]
4
晚景凄凉
莱布尼茨在终身为王公贵族们效劳以后,收到的报酬却是:疾病,迅速地衰老,被争吵搞得筋疲力尽,最后被踢了出去。1714年乔治到英国当国王没有带莱布尼茨。1716年,在经受了胆结石与痛风症的折磨之后,莱布尼茨离开了人世,据说只有忠实的秘书参加了他的葬礼。[1]
5
启示
莱布尼茨的动力来源是什么?一是对世俗功名的追求(热衷),二是对学问的求真精神(有抱负)。莱布尼茨是一个非常聪明的人,既获得了一些世俗的成功,学问也搞得非常出色。
莱布尼茨的成才之路令人神往,但政治上的失意(沦为弃子)也令人唏嘘。如果莱布尼茨不执着于追求名利,或许他可以在数学上做出更大的贡献,抑或者收获更多实现人生价值的幸福感。当然作为数学家,莱布尼茨已然是非常成功的。
莱布尼茨的一生及其治学精神值得我们反复回味和思考。一个人,他具有在任何时候、任何地点、任何条件下工作的能力,他不停地读着、写着、思考着,他的很多学术成果是在马车上完成的。于个人,可见成才不是看环境如何,而是有无坚定的理想抱负、有无甘愿坐冷板凳的决心。
二、莱布尼茨的微积分建立过程
早在1666年,莱布尼茨在《论组合的艺术》一书中讨论过数列问题并得到许多重要结论,这时还没有研究微积分问题。
从1672年大约开始,莱布尼茨将他对数列研究的结果与微积分运算联系起来。莱布尼茨后来在致洛必达的一封信中总结说:这使他发现,“求切线不过是求差,求积不过是求和”!
1673年,莱布尼茨提出自己的特征三角形概念,并应用它确实很快地发现了后来才“在巴罗和格列高里的著作中见到的几乎所有定理”。莱布尼茨还在关于特征三角形的研究中认识到:求曲线的切线依赖于纵坐标的差值与横坐标的差值当这些差值变成无限小时之比;而求曲线下的面积则依赖于无限小区间上的纵坐标之和(纵坐标之和在这里是指纵坐标乘以无限小区间的长度再相加,因而也相当于宽度为无限小的矩形面积之和)。莱布尼茨还看出了这两类问题的互逆关系。[2]
自此之后,莱布尼茨在微积分方法的建立和应用上又做了很多开拓性工作(见图2)。

图2 莱布尼茨的微积分建立过程
早期,莱布尼茨的这些研究都随手记录,故他的手稿散乱且难懂。大约到17世纪80年代初,莱布尼茨开始总结自己陆续获得的结果,并将它们整理成文,公诸于众。
莱布尼茨的微积分建立过程,呈现什么样的阶段特点?这是一个值得琢磨的问题。
我们可以发现,莱布尼茨关于微积分的原理思想在1672-1673年的时间内已经基本形成。而在1674-1680年,莱布尼茨的精力主要放在微积分理论体系的建立和微积分方法的开拓上。大约80年代初,开始后期的整理。
莱布尼茨早期的微积分思想有哪些?这些思想是怎么形成的?莱布尼茨早期的微积分思想主要包含三个方面:从离散到连续;以直代曲;积分是微分的逆过程。当然这些思想形成的基础是无穷小(不可分量)。这些思想的形成,一部分是受前人成果的影响,如巴罗和帕斯卡早在莱布尼茨之前就已经开始使用特征三角形。还有一部分是出于莱布尼茨天才般的直觉和善用类比方法。
三、莱布尼茨的微积分思想
1
从离散到连续
莱布尼茨的微积分思想发源于其对数列的研究,进一步由离散类比到连续情形。
数列的求差与求和
想象眼前铺成一条台阶,每一阶相对于地面的高度为
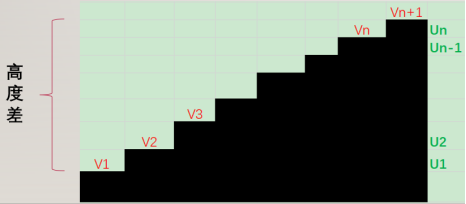
图3
差和分定义:设
定理1:(差和分基本定理)对于给定的一个数列
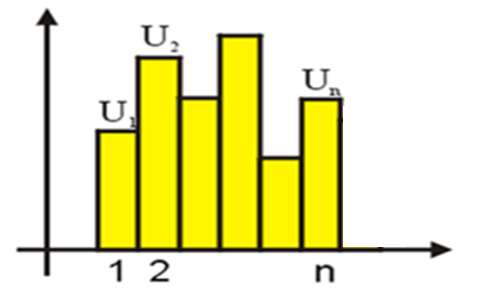
图4
定理1引出两个基本问题:
1. 研究差分在运算上的基本性质。
2. 已知一个数列
差和分的学习对于微积分的了解非常有帮助,因为两者不过是离散与连续之间的类推与观照而已。离散的差和分简单明了,再连续化就得到了微积分。[3]
函数的求差与求和
首先考虑面积函数
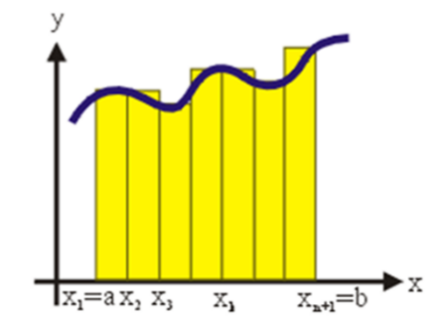
图5
差分变成微分、和分变成积分
现在想象将
因此,就用美妙的记号
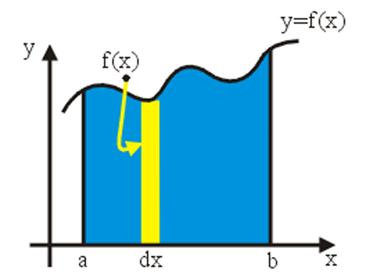
图6
从差和分基本定理到微积分基本定理
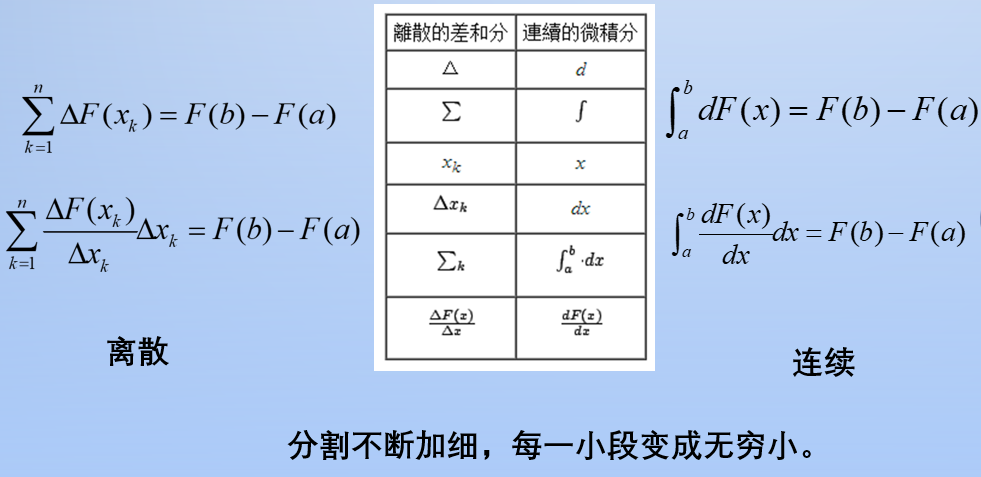
图7
微积分基本定理的一般描述:
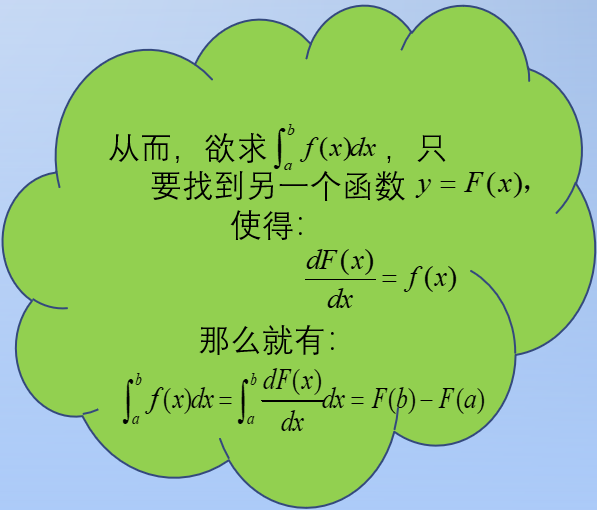
图8
莱布尼茨从离散到连续的微积分思想,从差和分基本定理到微积分基本定理,这里采用的就是类比思想。莱布尼茨天才地发现,“求切线不过是求差,求面积不过是求和”。数列和曲线下的面积函数(通过分割自变量区间)都具有求差和求和的特点。那么通过数列的离散版本的差和分基本原理,再借助无穷小,我们就得到了函数的连续版本的微积分基本定理。这里,无穷小
2
以直代曲
莱布尼茨的特征三角形,切线替代弧线,背后体现的是以直代曲的思想。这里先有切线,后定义
这里特征三角形的基本概念是无穷小,即微分,通过微商的形式刻画切线斜率。这里从运动角度来说,微商就是瞬时变化率。莱布尼茨对很多曲线应用特征三角形,得到了很多定理。莱布尼茨微积分理论的弊端在于讲不清楚无穷小究竟是什么。现代化的图示,微分不再是无穷小,而是关于增量

图9
3
积分是微分的逆过程
莱布尼兹假设可以求出一条曲线(称为割圆曲线),纵坐标为Z,使得
通过对积分进行微分和对微分进行积分,我们容易验证积分是微分的逆过程。但是需要区分莱布尼茨和牛顿微积分思想的不同:
在莱布尼茨的微积分体系中,核心概念是微分,导数是微商,而积分是微分的逆过程;在牛顿的微积分体系中,导数是核心概念,积分是导数的逆过程。
然而莱布尼茨的微分存在比较大的争议,因为有时把它当作是不可分量或者称作相邻两点之差,有时又把它当作要多小就有多小的量;同时牛顿的导数定义存在逻辑上的漏洞而一度受到贝克莱的责难。二人所建立的微积分体系都有难以说清的不足,后面才出现以极限理论为核心的微积分体系完成严格化这一工作。
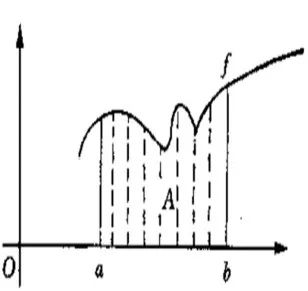
图10
引用文献
[1]贝尔著,徐源译.数学大师:从芝诺到庞加莱[M],上海科技教育出版社,107-138.
[2]李文林.数学史概论[M]. 高等教育出版社(第三版),2010:166-174.
[3]蔡聪明. 莱布尼兹如何想出微积分.公众号数学纵贯线.
转载内容仅代表作者观点
不代表中科院物理所立场
如需转载请联系原公众号
来源:数学经纬网
编辑:Garrett
| 留言与评论(共有 0 条评论) “” |