在视频分形:曼德勃罗集的眼泪里边,展示了曼德勃罗集变化为一滴眼泪形状的过程。
叫它“反演变换”,是因为它很像实数里的心形线变化为眼泪形状,就是把极坐标的公式分子分母交换一下位置:
转变为:
我们依葫芦画瓢,把曼德勃罗集的公式:
改为:
就可以了。
它的形状变画如图所示。


这里需要注意的是1/c是复数,所以要按复数的运算法则来计算。
假设c=a+bi,那么1/c应为:
就是c的共轭复数除以c的模的平方。
另外,如果把1看作是一个复数:(1+0i),我们也可以套用复数的除法来求解:
(a+bi)/(c+di)=(ac+bd)/(c2+d2) +((bc-ad)/(c2+d2))i
于是,我们只要修改材质里面的代码就可以了(可参考之前的文章)。
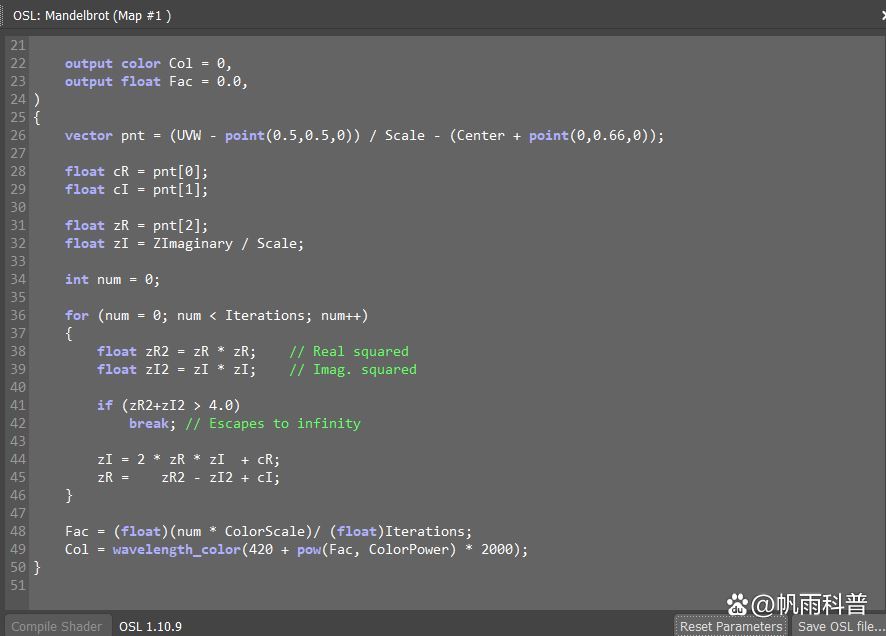
图中是3ds max自带的曼德勃罗集shader,里面的cR和cI(28、29行)就是c的实部和虚部,把它们修改成倒数就可以了。这是osl语言,其他软件也能使用,比如blender、maya等。
接下来就是要解决它的渐变过程,逐渐的变化才能形成动画,否则就是突然变化。
c变为1/c,有好几种方法,这里介绍两种:
c*a+(1/c)*(1-a),a由0变化到1c^a,a由1变到-1
| 留言与评论(共有 0 条评论) “” |